2. Linear Regression 본문
#Comment
## Notation
# Explanatory variables : X = t(x1,x2,...,xp)
# Real-valued response : Y
# Training data : D = {(xi,yi)|i=1,..n}
# General model : Yi = f(xi)+입실론i, e~N(0,sigma^2)
# Estimate the regression function : f(x).hat = E(Y|X)
# 즉 X가 주어졌을 때 y의 기대값으로 function을 추정하는게 핵심
##Variable
# y가 가질 수 있는 값을 실수 -oo ~ oo까지
# x가 가질 수 있는 값은
# 1 quantitive input(X), 2 categorical(dummy codig을 통해)
# 3 interaction(X1*X2), 4 transfomation of quantitive input(log),
# 5 Basis expansion(X2 = X1^2)
##Coefficients
# Motivation : 각 독립변수가 종속변수에 얼마나 기여하는지 알 수있는 척도
# 즉 앞선 f(x).hat은 coefficients beta를 추정하는 문제임
# x는 data로 이미 주어져있으므로
# How find beta : RSS(=SSE)를 통해 RSS를 최소화하는 beta를 찾는 것이 핵심
# RSS(beta) = sum((yi - f(xi))^2) 즉 오차의 제곱
# = Sum((yi - beta0 - sum(beta_j*x_ij))^2) (summary 1.1 )
# 그럼 우리가 추정한 beta는 무엇이고 어떤 통계적 성질을 따를까?(summary 1.2 )
# beta를 추정했으면 우리는 beta에 대한
# 점추정,구간추정,가설검정을 한다 어떻게 할까? (summary 1.3)
## Model
# beta를 하나하나 추정해서 유의한 coefficient인지
# t-test를 진행할 수 있지만 시간이 너무 오래걸린다
# model 자체에 대해 유의한 모델인지 검정하려면 어떻게 할까?(summary1.4)
## Singularity of t(x)x
# t(x)x가 non singular(n=p)여야만 determinant가 정의되고 역행렬이 정의됨
# but p>n상황에서는 역행렬이 정의가 되지 않는다 그러면 어떤 문제가 생길가?
# 1. beta.hat = solve(t(x)x)t(x)가 정의되지 않음
# 2. var(beta.hat) = sigma^2(I - H) -> sigma^2solve(t(x)x)로 var가 엄청커짐
# 어떻게 해결해야할까?
# 1. subset selection : 변수끼리 cov가 큰 변수들은 뺌으로써 p를 줄임
# 1) Forward selection : beta0 부터 시작해서 현재 model과 비교하며
# significant한 variable을 하나하나 추가
# 2) Backward elimination : 모든 변수들을 넣고 현재 model과 비교하며
# 하나하나씩 변수를 제거
# 3) Steowise regression : Forward와 backward를 합침 각 step에서
# 변수를 추가하거나 제거 그리드방법
# 2. regularization or penlization : ridge regression & LASSO
# 3. PCR : 변수 x의 선형결합으로 중요한 변수를 만들어 변수의 수를 줄임# 0. Install "ISLR2" package
install.packages("ISLR2")
library(ISLR2)
?Boston
dim(Boston)
names(Boston)
head(Boston)
# 1. Simple Linear Regression
lm.fit = lm(medv ~ lstat, data=Boston)
#The attach function allows to access variables of a data.frame
#without calling the data.frame.
attach(Boston)
detach(Boston)
#dependent variable y is medv and indepentent variable x is lstat
lm.fit = lm(medv ~ lstat)
summary(lm.fit)
#what is the name of independent variables x
names(lm.fit)
#what is the coefficients
lm.fit$coefficients
# star가 많을 수록 significant variables
coef(lm.fit)
confint(lm.fit) #2.5% is inf and 97.5% sup
#lm.fit is function, newdata is new x
predict(lm.fit, data.frame(lstat=c(5,10,15)), interval = "confidence")
predict(lm.fit, data.frame(lstat=c(5,10,15)), interval = "prediction")
#lstat와 medv의 관계를 보여주는 scatter plot
plot(lstat, medv)
# fittig 한 직선(model)
abline(lm.fit, col='red', lwd=2)
par(mfrow=c(2,2))
#1x1 independent variable와 dependent variable의 linearity 확인
#1x2 residual이 nomarlity을 띠는지
#2x1 residual이 homogeneity of variance를 띠는지
#2x2 outlier과 influential point를 찾기 위해
plot(lm.fit)
par(mfrow=c(1,1))
plot(predict(lm.fit), residuals(lm.fit))
plot(predict(lm.fit), rstudent(lm.fit))
#leverage value를 찾아주는 함수
#leverage value : 실제 종속변수 값 y가 예측치 y.hat에 얼마나 영향을 미치는지
plot(hatvalues(lm.fit))
which.max(hatvalues(lm.fit))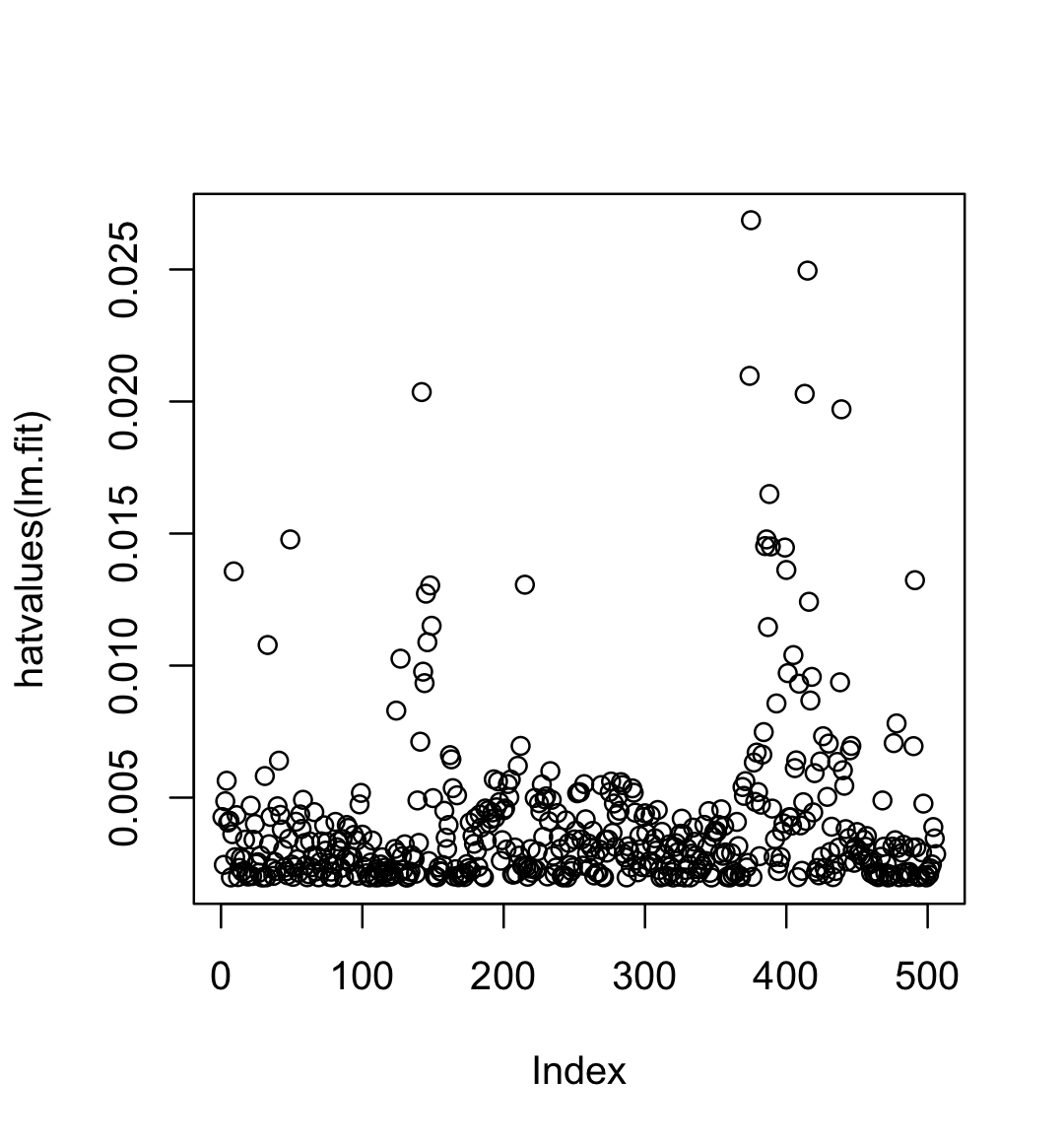
## 2. Multiple Linear Regression
lm.fit = lm(medv ~ lstat + age, data=Boston)
summary(lm.fit)
## Estimate beta manually?
y <- medv
one <- rep(1,length(y))
x <- cbind(one,lstat,age)
head(x)
dim(x)
## Predict medv manually for a new case with lstat=12, age=70 ?
beta.hat <- solve(t(x)%*%x)%*%t(x)%*%y
hat.matrix <- solve(t(x)%*%x)%*%t(x)
beta.hat <- hat.matrix%*%y
t(beta.hat)%*%c(1, 12, 70)
#~. all variables select
lm.fit = lm(medv ~., data=Boston)
#H0 : variable coefficient = 0 vs H1 : variable coefficient =! 0
#*** 이 많을수록 sigificant variable
summary(lm.fit)
summary(lm.fit)$r.sq
library(car)
vif(lm.fit)
# all variables중 age variable만 빼고 fitting
lm.fit1 = lm(medv ~.-age, data=Boston)
summary(lm.fit1)
# fittig model에 age variable을 넣고 다시 fittig
lm.fit1 = update(lm.fit, ~.+age)
summary(lm.fit1)
?update
## 3. Interaction Terms
summary(lm(medv ~ lstat*age, data=Boston))
## 4. Non-linear Transformations of the Predictors
lm.fit2 = lm(medv ~ lstat + I(lstat^2))
summary(lm.fit2)
#fit과 fit2 중 어떤 모델이 적합한지
lm.fit1 = lm(medv ~ lstat)
#H0 : coefficient of I(lstat^2) = 0 vs H1 : =! 0
anova(lm.fit, lm.fit2)
#H0 reject
## 5. Qualitative Predictors
?Carseats
dim(Carseats)
head(Carseats)
names(Carseats)
lm.fit = lm(Sales ~.+Income:Advertising + Price:Age, data=Carseats)
summary(lm.fit)
attach(Carseats)
contrasts(ShelveLoc)
## 6. Subset selection
?Hitters
names(Hitters)
dim(Hitters)
# Predict a baseball player’s Salary
# By various statistics associated with performance in the previous year.
Hitters$Salary
#missing value 확인
sum(is.na(Hitters$Salary))
#missing value 제거
Hitters <- na.omit(Hitters)
colnames(Hitters)
#model fitting
lm.fit <- lm(Salary ~., Hitters)
summary(lm.fit)
# 6.1 Best subset selection
install.packages("leaps")
library(leaps)
# regsubsetets is model selection function
regfit.full = regsubsets(Salary ~., Hitters)
length(colnames(Hitters))
summary(regfit.full)
#nvmax = 19 : all variable은 20개인데 최대 19개 까지에 대해서만 subset해라
regfit.full = regsubsets(Salary ~., data=Hitters, nvmax=19)
reg.summary = summary(regfit.full)
#model의 evaluation는 무엇으로 할건인지
names(reg.summary)
#Rsquare 방식으로 평가할 것이다
reg.summary$rsq
par(mfrow=c(1,1))
#SSE(sum of square error) = RSS(residual sum of square)
#변수의 수가 많을 수록 RSS는 낮아짐
plot(reg.summary$rss, xlab="Number of Variables ", ylab="RSS", type="l")
which.min(reg.summary$rss)
points(19, reg.summary$rss[19], col="red", cex=2, pch=20)
#Adj Rsquare방식은 변수 수에 대한 패널티를 부여
#Rsquare = SSR/SST이므로 총변동 중에 설명된 변동이 얼만큼이냐
#즉 높을수록 좋음 -> SSR/SST = 1-SSE/SST 여기에 자유도에 대한
#패널티를 부여한 것이 Adj Rsquare이므로 이것도 높을 수록 model이 data를 잘 설명한다는 뜻
plot(reg.summary$adjr2, xlab="Number of Variables ", ylab="Adjusted RSq", type="l")
which.max(reg.summary$adjr2)
points(11, reg.summary$adjr2[11], col="red", cex=2, pch=20)
#cp가 작을수로 model이 정확
plot(reg.summary$cp, xlab="Number of Variables ", ylab="Cp", type="l")
which.min(reg.summary$cp)
points(10, reg.summary$cp[10], col="red", cex=2, pch=20)
#bic가 작을수록 model이 정확
plot(reg.summary$bic, xlab="Number of Variables ", ylab="BIC", type="l")
which.min(reg.summary$bic)
points(6, reg.summary$bic[6], col="red", cex=2, pch=20)
#변수의 수가 많을수록 r2가 높으므로 0.55에서 모든변수
plot(regfit.full, scale="r2")
#변수의 수의 관계없으므로 adjr2가 가장 높은 변수 선택(검정)
plot(regfit.full, scale="adjr2")
#cp가제일낮은 value에서 변수 선택
plot(regfit.full, scale="Cp")
#BIC가 제일 낮은 value에서 변수 선택
plot(regfit.full, scale="bic")
#변수의 coefficient를 추출
coef(regfit.full, 6)

# 6.2 Forward & Backward selection
regfit.fwd = regsubsets(Salary ~., data=Hitters, nvmax=19, method="forward")
summary(regfit.fwd)
regfit.bwd = regsubsets(Salary ~., data=Hitters, nvmax=19, method="backward")
summary(regfit.bwd)
coef(regfit.full, 7)
coef(regfit.fwd, 7)
coef(regfit.bwd, 7)
## 문제 Compare forward selection models with
#predictors = 6 vs. #predictors = 7 by using anova
coef(regfit.fwd, 6)
coef(regfit.fwd, 7)
F.model <- lm(Salary ~ AtBat + Hits + Walks + CRBI + CWalks
+ Division + PutOuts, data = Hitters)
R.model <- lm(Salary ~ AtBat + Hits + Walks + CRBI
+ Division + PutOuts, data = Hitters )
#anova할때는 RMmodel을 앞에 쓰기
anova(R.model, F.model)
#not reject H0
#fullmodel is not significant model
'Applied > Statistical Learning' 카테고리의 다른 글
| Chapter 8 - 1 : Tree Based Methods (0) | 2024.01.17 |
|---|---|
| Chapter 7 - 2 : Support Vector Machine (0) | 2024.01.08 |
| Chapter 7 - 1 : Support Vector Machine (0) | 2024.01.08 |
| ISL sol & ESL sol (0) | 2024.01.04 |
| 1. Data Exploration (0) | 2023.05.05 |


